Turbulence Model¶
Overview¶
Accounting for atmospheric turbulence in infrared and optical wavelengths is important to AFSIM laser propagation because it produces an average beam spreading effect, independent of other considerations like diffraction and wavefront error, that reduces the average beam power impacting a high-energy-laser target or laser communications receiver.
Turbulence Model Equations¶
AFSIM implements the isoplantic relation for turbulent beam spread angle:
![\theta_0 = [2.91 k^2 \int_{0}^{L} C_n^2(z) z^\frac{5}{3}dz]^\frac{-3}{5}](../_images/math/2a990ac489a0c4e2a3b7b165e55d58061da5c3c2.png)
where 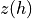 is a function relating altitude,
is a function relating altitude, 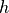 , to the distance along the path from receiver to transmitter, with length
, to the distance along the path from receiver to transmitter, with length 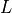 .
. 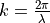 is the wave number for characteristic laser wavelength
is the wave number for characteristic laser wavelength 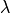 , and
, and 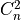 is the atmospheric structure parameter, having units of
is the atmospheric structure parameter, having units of 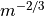 .
.
Note
When evaluating this integral it is understood that actual 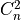 expressions are typically functions of
expressions are typically functions of 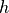 , not
, not  .
.
 Models¶
Models¶
There are various documented 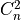 models. Currently implemented in AFSIM is the Hufnagel-Valley (5/7) (“hv57”) atmospheric structure function, which takes the form:
models. Currently implemented in AFSIM is the Hufnagel-Valley (5/7) (“hv57”) atmospheric structure function, which takes the form:
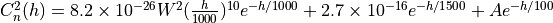
where 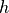 is the height above the surface where the function is computed (meters),
is the height above the surface where the function is computed (meters), 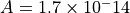 and
and 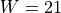 .
.
Reference¶
“The Effect of Atmospheric Optical Turbulence on Laser Communication Systems: Part 1, Theory” Thomas C Farrell, Air Force Research Laboratory, Space Vehicles Directorate 3550 Aberdeen Ave., SE, Kirtland AFB, NM 87117-5776; Unpublished

